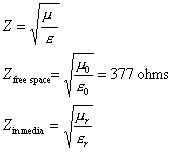How RF Anechoic Chambers Really Work

How RF Anechoic Chambers Work

By Glen Dash, Ampyx LLC, GlenDash at alum.mit.edu

A radio frequency “anechoic chamber” is a shielded room whose walls have been covered with a material that scatters or absorbs so much of the incident energy that it can simulate free space. Its origins can be traced to efforts to build aircraft which absorbed or scattered radar signals during the Second World War. Recent innovations such as the use of ferrite tiles, have greatly enhanced performance of these chambers.

Anechoic chambers may seem to operate through a bit of black magic, but the analysis of how they work is really quite straightforward. Assume for a moment that an electromagnetic plane wave (free space impedance = 377 ohms) strikes a wall at normal incidence. This can be modeled as a signal passing down a transmission line with a 377 ohm characteristic impedance as shown in Figure 1.

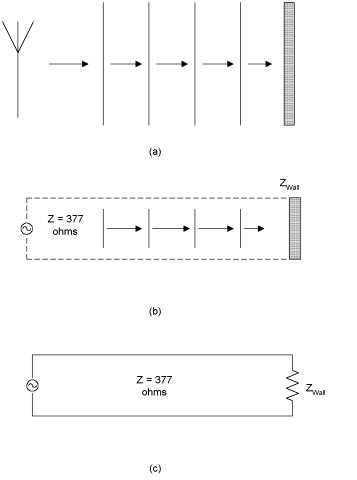
Figure 1: At (a), an antenna is shown radiating a plane wave that impinges on a metal wall at normal incidence. The antenna can be modeled as a voltage source and the resulting reflection computed using a transmission line circuit model as shown in (b) and (c).

To create a reflection-less chamber, we need, first of all, to understand how to send a signal down a transmission line and not have it reflect back. Since the shell of the anechoic chamber is metal, our transmission line model will have a shorted circuit at its termination. Since no energy is dissipated in our short circuit load, all of the signals sent down the transmission line will be reflected back. Our task is to find something put in front of the wall that absorbs or scatters this energy.

One of the methods first proposed to achieve this effect was through the use of the “Salisbury Sheet.” The Salisbury Sheet is a sheet of paper that had been coated with a substance to give it a surface resistivity of 377 ohms per square. It is placed exactly one-quarter wavelength away from the metal wall. The Salisbury Sheet makes the reflected signal virtually disappear.

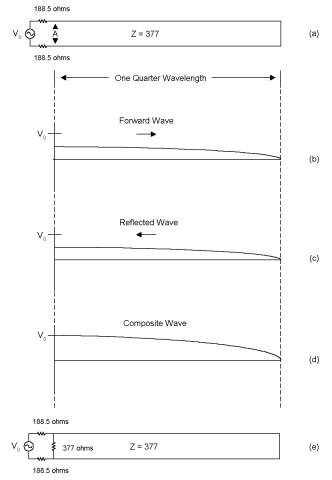
Figure 2: A shorted quarter-wavelength long length of transmission line (a “shorted stub”) has the impedance of an open circuit as seen from the source. By placing a resistor of 377 ohms near the source as in (e), the impedance as seen from the source can be changed to 377 ohms.

To see how the Salisbury Sheet works, look at Figure 2. Figure 2(a) shows a transmission line a quarter wavelength long with a characteristic impedance is 377 ohms. The load is a short circuit. Our voltage source also has a 377 ohm source impedance, divided into two resistors of 188.5 ohms each (Figure 2). When we turn the signal generator source on, a sine wave begins to propagate down the transmission line towards the load (Figure 2(b)). Since the characteristic impedance of the transmission line is also 377 ohms, the amplitude of this forward signal is reduced by half (at least initially) and is equal to V₀ /2. Reaching the load, a reflected signal is sent back. Because the transmission line is a quarter wavelength long, the reflected signal is exactly in phase with the transmitted one, and, as it passes backwards towards the source, the amplitude of the voltage along the transmission line doubles. At point A in Figure 2(a), exactly one-quarter wavelength away from the load, the transmission line has the impedance of an open circuit. For all practical purposes the transmission line is indistinguishable from no load at all -- it’s invisible.

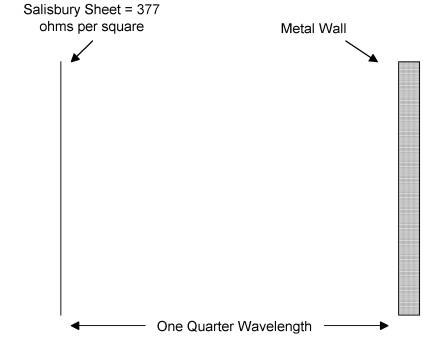
Figure 3: The Salisbury Sheet provides anechoic effects at one frequency. Placing a resistive sheet with an impedance of 377 ohms per square one quarter wavelength away from the wall results in impedance as seen from the source of 377 ohms.

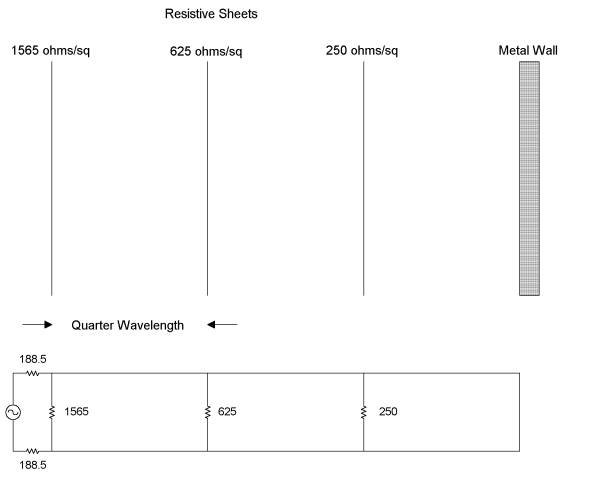
Figure 4: The use of several sheets of resistive paper widens the bandwidth of absorbent effects.

As elegant a solution as a Salisbury Sheet is, its limitations are obvious. It only works at one frequency. In order to make the Salisbury Sheet work over a larger range of frequencies, several sheets can be used as shown in Figure 4. Here sheets of different surface resistivities are placed at one-quarter wavelength intervals from the metal wall. The transmission line equivalent of such an arrangement is also shown. The arrangement reduces the reflection coefficient from 1 to less than .1 (equal to a reduction of reflected signal strength of greater than 20 dB), and it works over a 2.5 to 1 bandwidth centered on l.

Another approach is known as the “Jaumann Sandwich.” Here both the resistances and the distances from the metal wall are tapered (Figure 5(a)). Reportedly, the Jaumann Sandwich can achieve a 20 dB reduction in reflection over a 5 to 1 bandwidth (Reference 3).

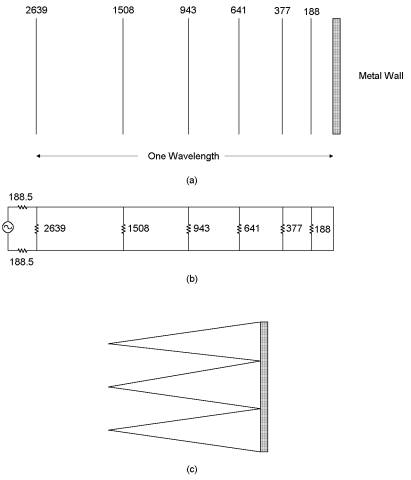
Figure 5: The Jaumann Sandwich uses a staggered array of resistive sheets and reportedly achieves a 20 dB reduction in reflected signal over a 5:1 bandwidth. For the case of normal incidence it can be modeled using the transmission line model in (b). Pyramidal absorbers use much the same effect to reduce reflection.

A modern implementation of theses tapered techniques employs pyramidal absorbers (Figure 5(c)). The tapered shape of the pyramidal material performs a role similar to the tapered resistances of the Jaumann Sandwich. Many small reflections are created as the electromagnetic wave passes into the pyramid and these reflections tend to cancel out. To be effective, however, the pyramids must be at least one half wavelength long at the lowest frequency of interest. The size of the pyramid needed to achieve this effect is mitigated somewhat by the fact that the wavelength of the radio frequency signal as it passes through the pyramidal material is shorter than the free space. It is reduced by a factor of:

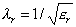
Where:

l_r= Wavelength in media (that is, within the absorber)

e_r= Permittivity relative to free space

Because of their size, providing for anechoic effects below 100 MHz requires the use of technologies other than pyramidal absorbers. In the last 20 years, ferrite tiles have become widely used as an absorbing mechanism. The key here is for the ferrite tile to present an impedance approximately equal to 377 ohms. This is accomplished by making sure the ratio of the permeability to the permittivity is equal to that of free space:

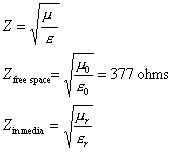
That, in turn, is achieved by keeping the ratio of m_r to e_requal to 377 ohms.

By itself that won’t prevent reflections however. What makes ferrite tiles work is that both the permeability and the permittivity are complex, so that the material is lossy. A typical ferrite material might have these properties:

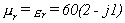
This results in a characteristic impedance of:

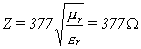
The complex permeability and permittivity results in loss as the wave passes through the ferrite tile. This loss is (Ref. 4):

The conductivity of the ferrite tile can be considered to be zero. At 100 MHz, the loss for a one-centimeter ferrite tile would be:

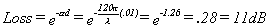
Therefore, as the wave passes through the ferrite tile, it is attenuated by 11 dB. As is reflects off the metal surface behind the tile, the wave is attenuated another 11 dB, for a total of 22 db of loss. Ferrite tiles will retain this absorbent effect at all frequencies for which the permeability and the permittivity retain these values.

By Glen Dash, Ampyx LLC, GlenDash at alum.mit.edu

References